TreeSet.

Serie - Fundamentos de Estrutura de Dados Elementar com Java.

TreeSet. Como funciona a Red-Black Tree.

O Desafio.

  As árvores, ou "Trees", em sua essência, representam estruturas facilmente compreensíveis. No entanto, algumas árvores, como a AVL Tree e a Red-Black Tree, envolvem implementações complexas. No caso do TreeSet, que utiliza o TreeMap, sua implementação se baseia na Red-Black Tree. Devido à natureza avançada desta estrutura, não abordarei detalhes profundos aqui. Dentre todas as estruturas, esta será a que simplificarei ao máximo, mas a simplificação será suficiente para fornecer noções básicas.

  Caso deseje explorar a implementação, recomendo estudar a RBTree apresentada no livro do Cormen, pois a RBTree utilizada no TreeSet é uma adaptação dessa presente no livro.

Como Funciona a Tree?

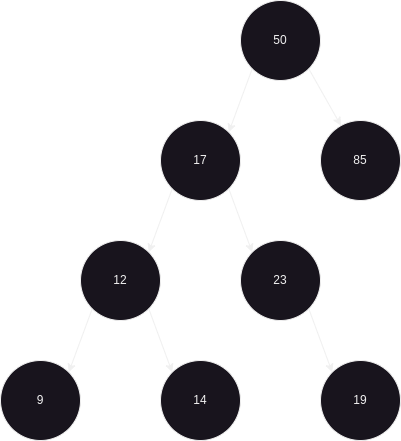
  Antes de mergulharmos na complexidade da Red-Black Tree, consideremos um exemplo mais simples de árvore: a Binary Search Tree (BST).

  Outro exemplo prático: suponhamos o conjunto {34, 84, 15, 0, 2, 99, 79, 9, 88, 89, 18, 31, 39, 100, 101}.

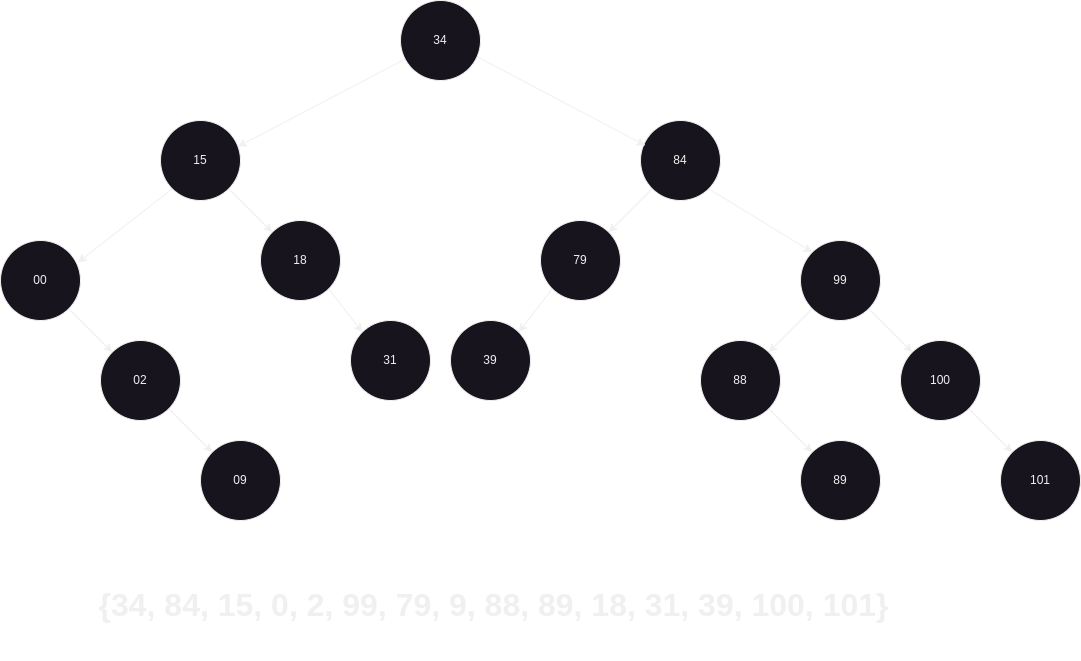
  Ao realizar uma pesquisa nesse conjunto, como, por exemplo, para o elemento 101, em um array seria necessário percorrer todos os elementos. No entanto, na BST, como evidenciado (veja o diagrama), percorreríamos apenas 4 elementos: 34 -> 84 -> 99 -> 100 -> 101. Isso é bastante eficiente, concorda?

  Observação: Ao apresentar um conjunto, significa que os elementos foram inseridos na ordem em que aparecem. Além disso, é importante destacar que demonstro o conjunto e, em seguida, como ele é organizado na árvore. Contudo, não entro em detalhes sobre por que a árvore se organiza dessa maneira, uma vez que, conforme especificado, não discutirei a implementação para melhor didática. Caso queira testar seus próprios conjuntos, consulte isso.

  No entanto, a BST (e outras Trees) apresenta um problema: ela pode facilmente se desequilibrar. A BST distribui os elementos menores à esquerda e os maiores à direita, seguindo a sequência de inserção. Em alguns casos, como o conjunto {99, 89, 100, 101, 102, 103, 104, 105, 106}, a árvore pode se tornar desbalanceada.

  Agora, pense: para encontrar o elemento 106, precisamos percorrer quase toda a árvore. Nesses casos, surge a necessidade de uma árvore de busca balanceada. Existem várias implementações que atendem a essa necessidade, e a utilizada no TreeSet é a Red-Black Tree.

Como funciona a RB Tree?

  A diferença fundamental entre a Red-Black Tree e a BST é que a RBTree possui um campo que "define as cores", sendo elas Vermelho (Red) e Preto (Black). Vale ressaltar que essas "cores" são representadas, na realidade, por um campo de 1 bit (boolean), geralmente associando o bit 1 à cor vermelha e o bit 0 à cor preta.

  A partir de agora, chamaremos os elementos da árvore pelo nome correto, que é "Nó" (Node)!

  O nó raiz (o primeiro) é sempre preto, e por padrão, ao criar um novo nó, ele será vermelho. A regra geral é que um nó vermelho só pode ter nós pais e filhos da cor preta. Os últimos nós (comumente chamados de "folhas") são nós vazios, que servem principalmente para garantir que os ponteiros dos verdadeiros últimos nós não sejam nulos, seguindo a regra das cores. A Red-Black Tree consegue reequilibrar esses nós por meio de rotações (basicamente, uma troca de ponteiros) de modo a manter a árvore bem balanceada. Veja um exemplo com nossos conjuntos anteriores ({34, 84, 15, 0, 2, 99, 79, 9, 88, 89, 18, 31, 39, 100, 101} e {99, 89, 100, 101, 102, 103, 104, 105, 106}):

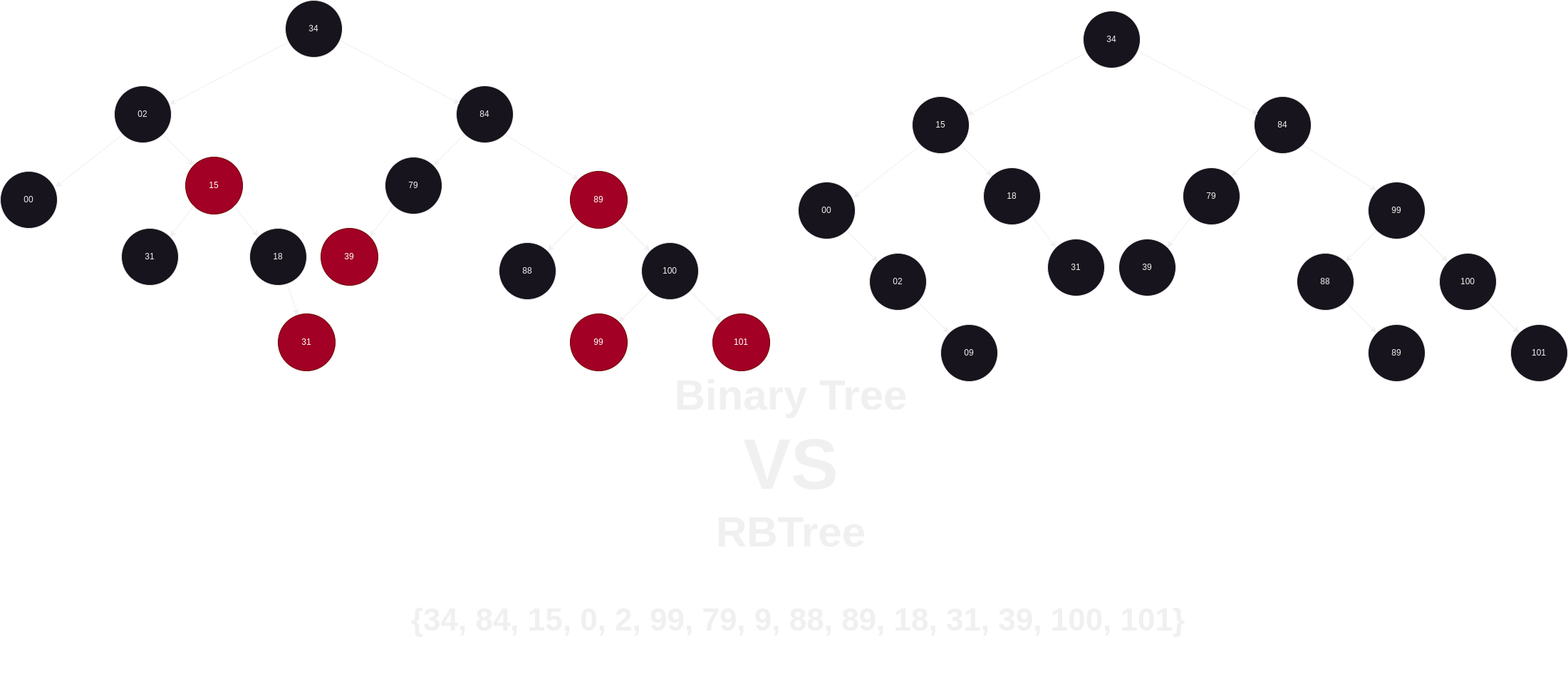
  no pior caso (note o balanceamente):

Ok. Mas e o TreeSet?

  O TreeSet opera com base nesse conceito, com a diferença de que não são permitidos nós repetidos. Além disso, no TreeSet, o conceito de Árvore Vermelho e Preta (Red-Black Tree) é estendido para manter a ordenação. Essa ordenação é mantida por meio de um conjunto que utiliza a ordem natural, quer um comparador explícito seja fornecido ou não. Dessa forma, temos o HashSet sem ordenação, o LinkedHashSet ordenando apenas por inserção e o TreeSet utilizando um Comparator.

Vantagens e Desvantagens

Vantagens

• 1 - Mantém os elementos em ordem natural ou com base em um comparador, permitindo a realização de operações eficientes de conjunto.
• 2 - Implementação de árvore Red-Black Tree eficiente.
• 3 - Suporta operações como encontrar o elemento sucessor ou predecessor.

Desvantagens

• 1 - Operações de inserção, remoção e pesquisa podem ter desempenho ligeiramente inferior em comparação com HashSet (apenas para os melhores casos).
• 2 - Ocupa mais espaço que HashSet devido à necessidade de armazenar nós adicionais na árvore.

Uso comum

  Manutenção de elementos ordenados em uma coleção, útil em cenários que exigem iteração em ordem.

  Cenário de uso: Em um sistema de calendário, um TreeSet pode ser usado para armazenar os compromissos agendados, garantindo que eles sejam recuperados e exibidos na ordem correta.